大地座標系統與二度分帶座標
將地球展平|分帶的迷思|座標系統範例說明|TWD67 與 TWD97 比較|座標概略轉換公式
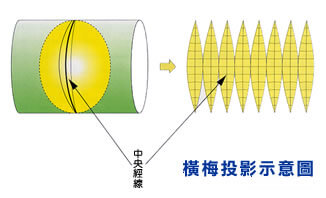 橫梅投影法、中央經線示意圖 |
橫梅投影的幾個專有名詞中央經線:圓柱面與地球相切於一條子午線上,稱為「中央經線」。在這條經線上,投影面與地表是密合相切的,其圖形變形量最小。不同的投影帶,其中央經線也不同,投影後各有其座標系統,無法直接拼接。 中央經線尺度:中央經線與圓柱面相切密合,所以尺度為 1,造成圖面其它地方被放大。為讓尺度變化較為均勻,於是將投影座標乘以某一常數,讓中央經線的尺度略小於1,逐漸往兩側放大,到投影帶中間某一部分尺度約為 1,投影帶邊緣則略大於 1,這個乘常數,我們便稱做「中央經線尺度」。 橫座標平移量:為避免讓中央經線西側座標出現負數,而將投影座標加一個常數,即為「橫座標平移量」。 |
談到座標系統,就必須先從「地圖投影」說起。地球是一個球體,球面上的位置,是以經緯度來表示,我們把它稱為「球面座標系統」或「地理座標系統」。在球面上計算角度距離十分麻煩,而且地圖是印刷在平面紙張上,要將球面上的物體畫到紙張上,就必須展平,這種將球面化為平面的過程,稱為「投影」。
經由投影的過程,把球面座標化算為平面直角座標,便於印刷與計算角度與距離。由於球面無法百分之百展為平面而不變形,所以除了地球儀外,所有地圖都有某些程度的變形,有些可保持面積不變,有些可保持方位不變,視其用途而定。
將地球展平
目前國際間普遍採用的一種投影,是 Transverse Mercator Projection (即橫梅投影、橫麥卡脫投影),屬於正形投影的一種,在小範圍內保持形狀不變,對於各種應用較為方便。我們可以想像成將一個圓柱體橫躺,套在地球外面,再將地表投影到這個圓柱上,然後將圓柱體展開成平面。圓柱與地球沿南北經線方向相切,我們將這條切線稱為「中央經線」。在中央經線上,投影面與地球完全密合,因此圖形沒有變形;由中央經線往東西兩側延伸,地表圖形會被逐漸放大,變形也會越來越嚴重。
為了保持投影精度在可接受範圍內,每次只能取中央經線兩側附近地區來用,因此必須切割為許多投影帶。就像將地球沿南北子午線方向,如切西瓜一般,切割為若干帶狀,再展成平面。目前世界各國軍用地圖所採用之 UTM 座標系統 (Universal Transverse Mercator Projection System),即為橫梅投影的一種。係將地球沿子午線方向,每隔 6 度切割為一帶,全球共切割為 60 個投影帶。台灣與澎湖分別位於 UTM 第 51 帶與第 50 帶。
分帶的迷思
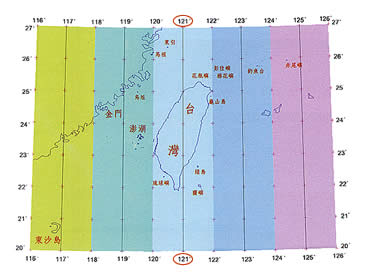 台灣地區二度分帶投影帶及中央經線分佈圖 台灣地區二度分帶投影帶及中央經線分佈圖
|
同樣是橫梅投影,為何又有「二度分帶」、「三度分帶」與「六度分帶」呢? 這是考量精度與涵蓋範圍大小之取捨,使得切割的帶狀寬度不同。切割越細,則越接近平面,其變形也就越小,但其拼接也會越麻煩,可謂魚與熊掌,不可得兼。UTM 設計時係以一百萬分之一的世界性輿圖為考量,涵蓋範圍頗大,且對精度要求較低,於是配合百萬分一輿圖之圖幅寬度,以六度為切割範圍。
由於早年涵蓋台灣地區中大比例尺之地形圖只有軍用地圖,因此一直以 UTM 座標作為地形圖的座標系統,即通稱之「六度分帶」。隨著各項經濟建設的蓬勃發展,對地形圖的運用日益增加,精度需求也提高,UTM 系統逐漸不敷使用。主要原因是台灣本島恰位於第 51 帶邊緣,是投影變形最嚴重的地區,西部平原距離投影的中央經線 123° 達 3 度,其投影誤差可達 1/2500,對寸土寸金的都市地區來說,根本難以接受,於是又有三度分帶座標系統的產生。
三度分帶是以 121° 為中央經線,適用於 119° 至 122°,台灣和澎湖都屬於同一投影帶,但在台灣西部平原的的比例誤差仍嫌過大,因此這個系統十分短命。
1974 年,政府為繪製五千分之一基本圖及地籍測量之需求,決定採用以 121° 為中央經線,圖幅可完整涵蓋台灣本島,橫跨經度二度的二度分帶座標。二度分帶顧名思義,是將地表每隔二度切為一個投影帶,因為切割更細,所以其投影誤差也更小(約 1/10000 左右),且台灣本島剛好都在同一投影帶內,不會造成使用上不便,因此一直沿用至今,成為國內製作各種圖籍標準,也因為切割較細,使得台灣、澎湖、彭佳嶼、釣魚台分別屬於不同投影帶。
座標系統範例說明
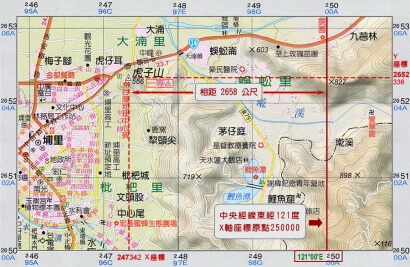 虎子山二度分帶座標與中央經線 121°E 距離示意 虎子山二度分帶座標與中央經線 121°E 距離示意 | |||||||||
範例說明:以南投埔里虎子山二度分帶座標為例:TWD67 247342mE,2652336mN,前面粗體字代表公里,後三碼代表公尺。橫座標表示它位在中央經線 121°E 以西 2 公里 658 公尺處 (即 250000-247342 = 2658),縱座標表示它距離赤道 2652 公里又 336 公尺。※取自 台灣地理人文全覽圖 北島篇第 51、52 幅 |
大地基準與座標格式
原則上,地表上任何一個地理位置都可以用大地基準 (Datum)+座標格式 (Format/Grid) 兩個參數來標示。在台灣常聽到的 TWD67、TWD97、WGS84 等,都是大地基準,而經緯度、UTM (六度分帶)、TM2 (二度分帶) 、電力座標等,指的是座標格式。 例如埔里虎子山原點,雖然有不同座標表示方式,指的都是同一個地理位置。
二度分帶座標範例說明
- 座標單位:是平面方格座標一種,利用 X、Y 軸座標值(十進位)來標示位置,單位是公尺,不同於球面經緯度座標(六十進位)以度分秒表示。
- 原點位置:X 軸座標原點,原應位在中央經線 121°E,如此台灣本島西側座標將出現負數,為確保整幅地圖座標值都是正數,於是將 X 軸座標原點,向西平移 250000 公尺。Y 軸座標原點位在赤道,其座標值即為相對於赤道的距離。
- 讀圖要領:將圖幅左下角視為原點,X 值向右為增加,表示您正往東行,Y 值向上為增加,表示您正往北走,X Y 值讀法為東距 (Easting)、北距 (Northing)。記得喔:向右讀、向上讀。
- 標記方式:先記 X 軸橫座標,再記 Y 軸縱座標 ,完整座標 X 值為六位數,Y 值為七位數,為避免混淆,請務必註明大地基準。例如玉山主峰座標:T67 244806mE, 2596536mN
TWD67 與 TWD97 孰是孰非
 台灣地理人文全覽圖 T67 座標控制基礎 |
平面基準:虎子山三角點 投影:橫麥卡脫 Transverse Mercator 參考橢球:1967 大地參考系統 GRS-67 座標系:二度分帶 TM 方格網 |
台灣地區的座標系統,從日治時期開始就已建立,經由陸續修測而得。(註:日治1910年起,採用 Bessel 1841 參考橢球體,ベッセル 1841 楕円體)。傳統是以天文觀測及三角測量的方式測定經緯度,由於受到地球重力場分佈不均勻等因素影響,所測得的經緯度只適用於台灣附近的局部區域。內政部於 1980 年公佈之 2662 點三角點,就是以這種方式測量的,為台灣現有多數圖籍之基準。這套座標系統是採用 1967 年的國際地球原子計算,通稱為「TWD67」。
衛星定位發明後,對於地圖測量技術起了至重大變革,不需再透過天文觀測,即可計算地表任何地方的經緯度,不僅精度更高,且所測得的是適用於全球的一套座標系統,我國亦順應世界潮流予以採用,將此座標系統稱為「TWD97」(Taiwan Datum 1997)。
簡而言之,TWD67 是只適用於台灣地區的座標系統,若要與其它國家銜接就會發生問題;TWD97 則與全球座標系統一致。兩者所採用的基準不同,所以同一地點在兩套系統中的座標就不會相同。
TWD67 與 TWD97 座標概略轉換公式
TWD67 與 TWD97 之間的差異量不小,若全面採用 TWD97,勢必導致大量舊有之圖籍全面改製,茲事體大,因此國內尚未全面採用。目前經建版地形圖仍採用 TWD67 系統,GPS 所測得的是 TWD97 系統。因此若將 GPS 測定的經緯度展繪到地形圖上,會發現有所偏差。有些接收器提供直接轉換為 TWD67 的功能,如果沒有此項功能,則須自行轉換。TWD67 與 TWD97 之間約有八百多公尺的差異,兩者之間並沒有簡單的公式可供轉換。但若要求精度不高,則可概略以下列公式換算之 (以二度分帶座標為例):
| TWD67 與 TWD97 座標概略換算公式 |
|---|
| TWD67 橫座標 = TWD97 橫座標 - 828 公尺 TWD67 縱座標 = TWD97 縱座標 + 207 公尺 |
上述公式誤差約在 5 公尺以內,對於工程應用或嫌不足,但對於一般 GPS 定位則是綽綽有餘。為了便於與現有地形圖對照,本圖集標示之座標皆為 TWD67 系統,原本打算加繪 TWD97 系統,但恐圖面過於紊亂而作罷。有了這些座標系統的基本概念,在使用本圖集時,就更能發揮其功能,迅速讓您知道身在何方了。(本公式為二參數轉換法,其它精度較高之轉換方式,如最小曲率法、三參數轉換、七參數轉換等,請參考:Taiwan Datums:轉換參數)
沒有留言:
張貼留言